
Numerical comparison of iterative methods for solving nonlinear equations. On some third-order iterative methods for solving nonlinear equations. An improved Regula Falsi method with quadratic convergence of both diameter and point for enclosing simple zeros of non-linear equations. On a class of quadratic convergence iteration formula without derivatives.

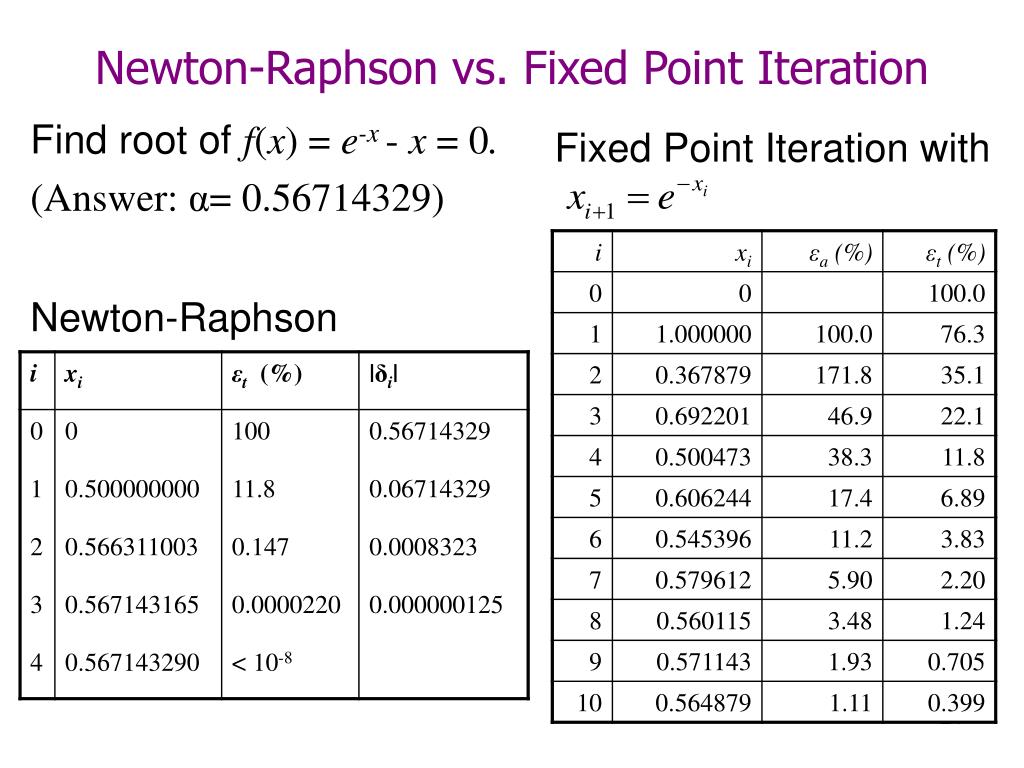
Fourth order derivative methods for solving non-linear equations. Example 4Ĭonsider a transcendental equation of the form Therefore, the proposed method is useful also for solving such the real life problem. Most of the real life problems take too much computational time for convergence because of the complex flow physics and higher degree polynomial equations. Thus, the proposed method is also efficient for error estimation. The error estimation after the 3rd iteration (Table 1), show that the proposed method having \(5.4\%\) error in comparison to Bisection ( \(20\%\)), Regula-Falsi ( \(9.57\%\)) and Newton–Raphson ( \(22.91\%\)) methods. Therefore, the proposed method is not only reduce the computational affords but also provide the guaranteed result for solving the real life problem. But one of the main advantage of proposed method is that it gives guaranteed result over the Newton–Raphson method. It is also clear that both of the methods (proposed and Newton–Raphson) are converged in 7th iteration. Thus proposed method is efficient over bisection and Regula-Falsi methods. It is found that bisection and Regula-Falsi methods converged after 22 and 14 iterations respectively (Table 1), while the proposed algorithm converged in 7th iteration. The order of converges of any iterative method is defined as
#MODIFIED NEWTON RAPHSON METHOD CALCULATOR MANUAL#
This algorithm would help to implement the manual calculations in commercial packages such as Maple, Mathematica, SCILab, Singular,etc. The implementation of the proposed algorithm in Matlab is also discussed (See, Additional file 1). Repeat steps I, II and III until we get required approximate solution. The value \(x_n\) in Eq. ( 6) gives the iterative formula with \(|f(x_\). The new proposed algorithm will work even the first derivative equals to zero where Newton–Raphson method fails.

In the present work, the proposed new algorithm is based on standard Regula-Falsi and Newton–Raphson methods, which provides guaranteed results and higher order convergence over Regula-Falsi method. It is clear from the survey, that the most of new algorithms are either based on three classical methods namely Bisection, Regula-Falsi and Newton–Raphson or created by hybrid processes. Many scientists and engineers have been proposed different hybrid models on Newton–Raphson method. However it does not always give guaranteed root. The order of convergence of Newton–Raphson method is two, therefore it converges very rapidly than other methods (Bisection, Regula-Falsi, etc.). the derivative of the function is zero or approximately zero. So this method fails where tangent is parallel to x-axis, i.e. The next approximate root is taken those value where the tangent intersect the x-axis. This method uses the concept of tangent at the initial approximation point. Newton–Raphson method is generally used to improve the result obtained by one of the above methods. Therefore, in the present work Regual-Falsi method has been used as its standard form with Newton–Raphson method and found better convergence. However, it is found that modified form of Regual-Falsi method becomes more complicated from computational point of view. Thus previously published works have revised/implemented Regula-Falsi method in several ways to obtain better convergence. This method gives guaranteed result but slow convergence therefore several researchers have improved this standard Regula-Falsi method into different hybrid models to speed up the convergence. Then these two points are connected through the straight line and next approximation is the point where this line intersect the x-axis. In Regula-Falsi method, two initial guesses are taken in such a way that the corresponding function values have opposite signs. It is well known that all the iterative methods require one or more initial guesses for the initial approximations. In the literature, there are some numerical methods such as Bisection, Secant, Regula-Falsi, Newton–Raphson, Mullers methods, etc., to calculate an approximate root of the non-linear transcendental equations. Analytical solutions of such non-linear equations are very difficult, therefore only numerical method based iterative techniques are the way to find approximate solution. In this reference, a number of methods have been proposed/implemented in the last two decades. Most of the real life-problems are non-linear in nature therefore it is a challenging task for the mathematician and engineer to find the exact solution of such problems.


 0 kommentar(er)
0 kommentar(er)
